Fukui functions shows the level of reactivity of different places in a complex molecule. They can be easily plotted with GabEdit software but it has a pure functions of chemical drawing. PyMol is a powerful drawing instrument and here we show how to plot Fukui function with PyMOL after two calculation steps with FireFly (PC-GAMESS).
Fukui function representing a reactivity for elecrophilic attack in a finite difference approximation is defined as following:
Thus, there are two ways to calculate this function for molecule M: easy and correct. Using easy way we assume M(N-1) having the same orbitals as M(N). Id est electrophilic Fukui for singlet molecule M is a half of HOMO density:
The correct way is to remove an electron and compute duplet cationic state electronic density in the geometry of neutral molecule.
Lets realize both techniques in FireFly using chlormethylbenzene molecule as an example.
Easy way: drawing HOMO orbital density
- At first we should optimize geometry of our molecule at some level of theory. We take RHF-MP2 method and 6-31(p,d) basis set. I used the following protocol:
$CONTRL SCFTYP=RHF EXETYP=RUN RUNTYP=OPTIMIZE COORD=UNIQUE MPLEVL=2 INTTYP=HONDO ICUT=11 ITOL=30 NZVAR=39 MAXIT=200 $END $STATPT NSTEP=100 $END $BASIS GBASIS=N31 NGAUSS=6 NPFUNC=1 NDFUNC=1 DIFFSP=0 $END $SYSTEM TIMLIM=2000 MWORDS=25 $END $GUESS GUESS=HUCKEL $END $SCF FDIFF=.f. DIIS=.t. ETHRSH=0.1 DIRSCF=.t. $END $P2P P2P=.t. DLB=.t. XDLB=.t. $END $ZMAT AUTO=.t. DLC=.t. $END
- At first lets draw HOMO density. To form cube file modify your geometry-optimization input adding following lines:
$ELDENS IEDEN=1 MORB=33 $END ! computing density of separate orbital no. MORB ! if MORB is not pointed - total density will be computed $CUBE nxcube=120 nycube=120 nzcube=120 ! number of steps in every direction x0cube=-6 y0cube=-6 z0cube=-6 ! start points xincub=0.1 yincub=0.1 zincub=0.1 ! step points of cube grid $END $GUESS GUESS=MOREAD NORB=33 $END
Then set RUNTYP=ENERGY and remove optimization-specific groups: $STATPT and $ZMAT. Then get $VEC group from PUNCH-file of the geometry-optimization run (you should take vector of the last point of course) and insert it after $DATA.
- After FireFly process last input we obtained PUNCH-file with $CUBE group inside. Copy the content of this group to the distinct file mo33.cube.
- Now lets draw it. Convert FireFly output into PDB file with babel:
babel -igamout output.log -opdb benz.pdb
Then load into pymol both PDB and CUBE files:
load benz.pdb, benz load mo33.cube, mo33
Now generate isosurface of molecular orbital and set surface opacity:
isosurface i0, mo33, 0.02 set bg_rgb, white set transparency, 0.5
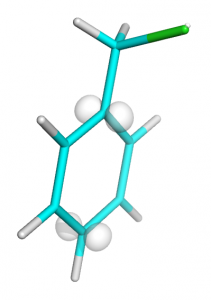
You should get an image like this:
The correct way: drawing electrophilic Fukui function
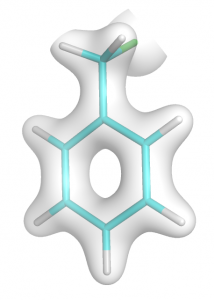
- At first generate total electron density using input from step no. 2 (easy-way). To compute total density don’t define MORB in $ELDENS group. Extract it to file benz.cube. If you draw it you will see image like this:
- Secondly, you should make single-point computation for cation molecule. To speed up SCF procedure using of $VEC as GUESS is strongly(!) recomended. Make input file on a basis of step no. 2:
$CONTRL SCFTYP=UHF ICHARG=+1 MULT=2 $END $GUESS GUESS=MOREAD NORB=33 $END
Now we want to use RHF vector for UHF calculation. So all orbitals should be repeated. Copy content of $VEC group and simpli paste it before $END of $VEC group.
- Extract CUBE to separte file cation.cube. Now we should subtract one cube from another. We will use free script written by Inaki Silanes, CubeDiff. You can download local copy of his script here. Making subtraction is very simple:
./cubediff.r97 +benz.cube -cati.cube > diff.cube
Next visualize diff.cube as it was described before:
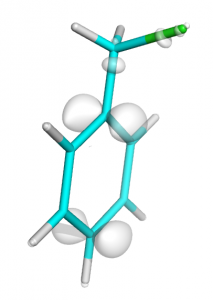
Total difference in electron density during ionization of clhormethylbenzene molecule (0.01 isosurface)
Note: here we draw 0.01 isosurface wereas in easy-way plot we drew 0.02 isosurface. Because total HOMO orbital have two electrons and should be divided by two (see equations at the beginning).