This script allows one to visualize normal modes, calculated with GROMACS package, using PyMol. In particular the script loads Hessian matrix from an .mtx file produced by Gromacs, solves for it’s eigenvectors and eigenvalues and prints them out, and finally produce several frames corresponding to selected vibrational mode. See related media in the end of the page.

The script depends on ctypes and numpy python libraries. Also you should have Gromacs shared library libgmx_d.so installed. Versions 5 and 6 of the latter lib are known to work. Change it’s path at line 6 and 7 of the script to the appropriate.

To use the script, save it to some file, then load it into PyMol:

PyMol> run /path/to/script.py

now load into PyMol a molecular system for which Hessian matrix has been calculated:

PyMol> load system.pdb 

now issue the following command

PyMol> nmgen obj, 0, mtx=system.mtx

it will load «system.mtx» file generated by Gromacs mdrun, solve for eigenvectors and print out eigenvalues (frequencies) along with their numerical ID’s in the first column. After this step the resulting data is associated with the object «obj» and will be reused for subsequent nmgen calls, if «mtx» argument is omitted. Now take a look at the resulting table and choose some mode. To generate selected mode labeled with «ID» issue:

PyMol> nmgen obj, ID

This will produce an object named «obj-ID», contaning 20 frames of the system oscillating along selected normal mode. Also the normal modes list is printed once again.

Finally here is the script:

from ctypes import *
from numpy import linalg,sqrt,dot,zeros,double,real,pi,sin,argsort,real
from pymol import cmd, stored
from pickle import dump

cdll.LoadLibrary('/usr/lib/libgmx_d.so.5')
gmx_mtxio_read = CDLL('/usr/lib/libgmx_d.so.5').gmx_mtxio_read

def loadmtx(mtx):
  nrow = c_int(0)
  ncol = c_int(0)
  hess = POINTER(c_double)()
#  hess = POINTER(c_float)()
  gmx_sparsematrix = POINTER(c_byte)()
  gmx_mtxio_read(mtx, byref(nrow), byref(ncol), byref(hess), byref(gmx_sparsematrix))
  ahess = zeros((nrow.value, ncol.value), dtype=double)
  for i in range(nrow.value):
    for j in range(ncol.value):
      ahess[i,j] = hess[i*ncol.value+j]
  return ahess

def nmgen(obj, nmid, mtx=None, amp=1., nframes=20, dump_file=False):
  """ 
nmgen - generate normal mode from GROMACS .mtx file

Usage: nmgen obj, nmid, [mtx=None, [amp=1.0, [nframes=20]]]

NB: * This script depends on GROMACS libraries. Check for libgmx_d.so.5 in /usr/lib. 
    * The script works with full (double) precision MTX files. 
      Slight modifications to script are needed to work with single precision files.

Example:
  Load structure
  >  load molecule.pdb

  Load appropriate mtx and generate normal mode #3
  >  nmgen molecule, 3, molecule.mtx

  Generate normal mode 7 with magnitude 3.0 A.
  No mtx file is specified since we have already loaded it for this structure.
  >  nmgen molecule, 7, amp=3.0
  """
  nmid = int(nmid)
  amp = float(amp)
  newobj = "%s-nm_%d" % (obj, nmid)
  genwv = 0
  cmd.delete(newobj)

  try:
    stored.NMA[obj]
  except AttributeError:
    stored.NMA = {}
    genwv = 1
  except KeyError:
    genwv = 1

  if genwv or mtx:
    if not mtx:
      print "Please specify gromacs MTX file"
      return 0
    stored.mass = {'H':1., 'C':12.,'N':14.,'O':16.,'M':24.3}
    hess = loadmtx(mtx)
    MI = 0.*hess
    stored.MI = MI
    cmd.iterate_state(1,obj,"stored.MI[(ID-1)*3,(ID-1)*3]=1./stored.mass[elem]")
    for id in range(hess.shape[0]/3):
      MI[id*3+1,id*3+1],MI[id*3+2,id*3+2] = MI[id*3,id*3],MI[id*3,id*3]
    w2,v = linalg.eig(dot(MI, hess))
    w = sqrt(w2)*1.e12
    stored.NMA[obj] = {}
    stored.NMA[obj]['hess'] = hess
    stored.NMA[obj]['w'] = w
    stored.NMA[obj]['v'] = v
    if dump_file: 
      f=open(dump_file, 'w')
      dump((hess,MI,w,v), f)
      f.close()
  else:
    w = stored.NMA[obj]['w']
    v = stored.NMA[obj]['v']

  si=argsort(w)
  print "%7s%20s%20s" % ('NMID', 'f Hz', 'f cm^-1')
  for i in range(w.size):
    print "%7d%20.5e\t%20.0f" % (i, w[si[i]]/2./pi, w[si[i]]*5.30884e-12),
    if i == nmid:
      print "*"
    else:
      print ""
  nm = real(v[:,si[nmid]])
  nm *= amp/sqrt((nm**2).sum())
  for ifr in range(nframes):
    cmd.create(newobj, obj, 1, ifr+1)
    stored.nm = nm*sin(2.*pi*ifr/nframes)
    cmd.alter_state(ifr+1, newobj, "x,y,z = x+stored.nm[(ID-1)*3], y+stored.nm[(ID-1)*3+1], z+stored.nm[(ID-1)*3+2]")
cmd.extend("nmgen", nmgen)

This is a visualization of Hessian matrix of a nanotube:

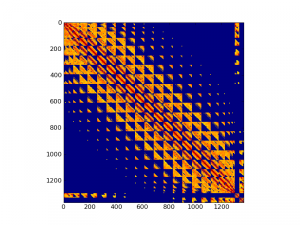
And here are some normal modes of carbon nanotubes, produced by the script: